Over the past year, NCTQ has been reaching out to mathematicians, math educators, and practitioners for the purpose of updating and streamlining the Elementary Mathematics standard in the Teacher Prep Review. First developed in 2008, there have been few modifications made to the standard. With this revision, NCTQ aims to give institutions a clearer set of guidelines for improving the math preparation provided to elementary teacher candidates based on the most recent research available. This brief describes the results of this external engagement process, which includes pilot testing of the proposed revisions, an open comment period in which we heard from over 275 math educators, as well as recommendations from both an expert advisory panel and a technical advisory group.
[rationale]
Rationale for standard
Not surprisingly, students taught by elementary teachers who themselves have relatively strong knowledge of mathematics make greater gains in math.332 Unfortunately, given the great variability in institutional course requirements in mathematics, completing neither a bachelor's degree nor a teacher preparation program guarantees that elementary teachers will have acquired the content knowledge needed for the job. There are few indications that the current approach works well. Most elementary teachers report not feeling well-prepared to teach many of the topics found in standard elementary curriculum, no doubt contributing to the persistent (and indeed worsening) performance on international math tests by students from the United States.333 While the U.S. ranks 9th in reading, it ranks 31st in math literacy on the international PISA test.334A number of studies looking at the critical connection between teacher and student knowledge provide important insights into how teacher preparation programs could improve the math knowledge of their teacher candidates.335 One clear recommendation is for the math coursework taken by elementary teacher candidates to be exclusively aimed at a teacher audience, not the broader campus population. There is solid consensus among both mathematicians as well as mathematics education organizations for the "teacher audience" approach, overriding concerns that such coursework might not be as rigorous as other math coursework, as it allows coursework to focus on elementary and middle school mathematics topics at a conceptual level. Both the National Council of Teachers of Mathematics (NCTM)336 and the Conference Board of the Mathematical Sciences (CBMS),337 recommend that aspiring elementary teachers take 12 semester credit hours in "elementary mathematics content" covering Numbers & Operations, algebra, measurement and data, and geometry.338
Further, this coursework should also be neither pure mathematics nor pure methods, but a combination of both.339 By designing courses that address both subject matter knowledge (including common content knowledge and specialized content knowledge) as well as pedagogical content knowledge (including knowledge of content and students and knowledge of content and teaching), institutions can best meet the needs of future teachers.340
[claim]
Claim
In order that elementary teachers are able to deliver equitable and effective mathematics instruction, teacher preparation programs provide their elementary candidates with both the content and pedagogical knowledge specified in commonly accepted mathematics education standards.[newscoring]
The new scoring approach
To determine if programs meet this claim requires examining all of the teacher-audience mathematics content and pedagogy courses required by either the institution at large (in "gen ed" requirements) or specifically by an educator preparation program. Relevant courses are identified through the course catalog and/or degree plans.The new scoring approach considers how programs dedicate instructional time across required coursework to each of four key mathematics topics: 1. Numbers & Operations; 2. Algebraic Thinking; 3. Geometry & Measurement; and 4. Data Analysis & Probability. Additionally, to mitigate the risk of courses dedicating too little time to the methods needed to teach each of these four topics well, the protocol also considers the instructional time dedicated to a fifth topic: Mathematics Pedagogy.
The protocol assesses each program against a set of recommended instructional hour targets, with each target capturing the minimum amount of time that needs to be allocated to deliver both the content and pedagogy teachers need.
While not far from previous guidance in the original standard in 2008,341 the targets have been slightly revised, incorporating the consensus of feedback received in the Fall 2021 Open Comment Period, including feedback from over 275 math educators, and the final recommendations of the Expert Advisory Panel.
[hourtargets]
Recommended instructional hour targets
| Numbers & Operations | Algebraic Thinking | Geometry & Measurement | Data Analysis & Probability | Math Pedagogy | Total |
| 45 hours | 20 hours | 25 hours | 15 hours | 45 hours | 150 hours |
| One full 3-credit course | Just under half of a 3-credit course | Just over half of a 3-credit course | One-third of a 3-credit course | One full 3-credit course | 10 credits |
After making necessary adjustments to accommodate the variations in course systems of credit hours used across 1,000 institutions, course time is converted into instructional hour counts and summed across all relevant courses. These results are then compared to the minimum instructional hour targets.
To determine the instructional hours dedicated to each topic, analysts apply the scoring protocol described below, coding one of two available artifacts, either a course description or a course syllabus for each of the required courses. When using course descriptions, two analysts code each independently, bringing in a third analyst to adjudicate any significant differences. When using course syllabi (which typically contain more information), one analyst codes the syllabus, with multiple analysts coding a random sample of 20% to provide for real-time monitoring of interrater reliability.
Basic coding structure
| When coding a Course Description | When coding a Syllabus | ||
| Reference Count | Count of the total number of references to each identifiable topic (e.g., Numbers & Operations). | Unit Type | Identify the type of calendar (daily, weekly, etc.) used in the syllabus. |
| Unit Count | Identify the total number of units (days, weeks, etc.) that are defined in the course schedule. | ||
| Reference Count | For each unit, count of the total number of references to each identifiable topic. | ||
| Within the course description or details presented in the syllabus... |
Within each unit specified in the syllabus...
|
||
| 1. Numbers & Operations | Count of the number of references to Numbers & Operations including any subtopics within that domain. | ||
| 2. Algebraic Thinking |
Count of the number of
references to Algebraic Thinking, including any subtopics with that domain. |
||
| 3. Geometry & Measurement | Count of the number of references to Geometry & Measurement including any subtopics with that domain. | ||
| 4. Data Analysis & Probability | Count of the number of references to Data Analysis & Probability, including any subtopics with that domain. | ||
| 5. Mathematics Pedagogy | Count of the number of references to mathematics instructional approaches. | ||
|
6.
Other Content Topics |
Count of the number of references that address mathematics content topics outside any of the four content areas (e.g., references to trigonometry or calculus). | ||
| 7. Other Pedagogy Topics | Count of the number of of references that address general pedagogy or subject-specific pedagogy for subjects other than mathematics. | ||
Grading protocol
The Expert Advisory Panel provided recommendations for the distribution of grades based on how close (or far) the required coursework came to meeting the targets in all five areas. The Panel recommended that programs achieve at least 90% of the target instructional hours in each topic area to earn an A. The total percentage of instructional hours to earn each grade is noted below.
| Grade | Total Percentage of Instructional Hours Target |
| A+ | 100% of the instructional hours target in each of the five topic areas. |
| A | 90% or more of the instructional hours target in each of the five topic areas. |
| B | 80% or more of the total instructional hours target across all topics (rather than in each topic area). |
| C | 70% - 79% of the total instructional hours target across all topic areas. |
| D | 60% - 69% of the total instructional hours target across all topic areas. |
| F | Less than 60% of the total instructional hours target across all topic areas. |
Programs may earn similar grades with different strengths and weaknesses. In order to support program improvement and an understanding of where gaps may exist, programs will be provided detailed feedback on how their program fared in each of the five topic areas.
Sample Analysis for a Program Earning a B
|
|
Numbers & Operations |
Algebraic Thinking |
Geometry & Measurement |
Data Analysis & Probability |
Mathematics Pedagogy |
Total Hours |
Percentage of target instructional hours met |
Grade |
| Total hours across coursework | 45 | 18 | 25 | 0 | 35 | 123 | 82% | B |
| Instructional Hour Targets | 45 | 20 | 25 | 15 | 45 | 150 |
This example shows how a sample program earned a grade of B. It met 82% of the overall instructional hours recommended or 123 out of 150 hours.
Because the standard seeks to address whether or not programs are providing minimal coverage, instructional hours above the individual topic targets are not considered in the scoring protocol. For example, if a program has more than 25 hours dedicated to Geometry & Measurement, those hours are not considered in the overall total hour calculation.
One notable scoring exception proved necessary. For purposes of grading, the number of hours estimated for both Numbers & Operations and Algebraic Thinking is combined. Coursework descriptions often combine Numbers & Operations and Algebraic Thinking making it difficult to separate when determining overall grades for teacher preparation programs. This may occur because student standards (such as the Common Core State Mathematics Standards (CCSS-M)) combine Operations and Algebraic Thinking through the mid-elementary grades, with Algebra becoming more of a separate topic in later grades. While both categories are coded individually, the total hours are combined to ascertain whether the program is meeting the intended instructional hour target. For example, if a program dedicates 50 hours to Numbers & Operations and 15 hours to Algebraic Thinking, the program is considered to have met the total target of 65 hours across both topic areas.
[compare]
Comparing the revised standard to the original math standard
There are three significant changes being made in this new standard.First, unlike the previous standard, the protocol now permits rendering judgments using only a course description, provided institutions have the opportunity to supply course syllabi once they have reviewed their initial grade.
NCTQ conducted a number of pilot tests to assess the accuracy of course descriptions before making this determination. A pilot test evaluated 200 courses where both course descriptions and syllabi were available to arrive at two independent assessments for how much time was spent on each of the five key topics. The two analyses produced similar results on average, within a range of 10 percentage points for each of the five topics. Further, the distribution of program grades under the two approaches was highly correlated, with no notable bias towards either approach. The use of course descriptions in lieu of course syllabi, along with issues pertaining to interrater reliability when using one or the other, was reviewed by the Technical Advisory Group (TAG) and elicited no substantial concerns, provided programs had the opportunity to submit additional evidence if a score was based only on a course description. More details can be found here and subsequently in the technical manual with the full release of the standard.
Second, the revised standard will no longer consider textbooks when determining the sufficiency of a course. Previously, the textbook accounted for a significant portion of a program's grade. This decision was based on previous feedback that without an accompanying syllabus, it was not possible to know what chapters in a textbook were being covered. The Expert Advisory Panel also supported this decision without reservation.
Lastly, math pedagogy is now incorporated as a major topic area along with the four major content topic areas, whereas previously a math methods course only counted towards the program's grade if all of the content thresholds were met.

[Section2]
Summary of Open Comment Period Responses
To gather broader input from the education field, NCTQ conducted an "open comment period," publishing the draft plans for the new Elementary Mathematics standard and inviting feedback on specific aspects, as well as any general feedback.
[responses]
Who responded during the open comment period?
The open comment period was open from September 20 through October 15, 2021. Notices about the open comment period were emailed to state education agencies, leaders of teacher preparation programs, math faculty at teacher preparation programs, advocacy groups, state teachers' union leaders, state school board members, state legislators on education committees, state governors' education policy advisors, superintendents and chief academic officers of the nation's 500 largest school districts, and other potentially interested parties. This totaled over 14,000 contacts. The open comment period was also advertised through NCTQ's monthly newsletter, the Teacher Quality Bulletin, which has a subscriber list of 6,400 individuals.We received 275 responses to the online survey, in addition to several responses emailed directly to NCTQ. The majority of respondents (65%) were from teacher preparation programs; another 16% were from institutions of higher education external to the teacher preparation program, and 9% were from state education agencies. Most respondents (81%) reported that they have at some point taught a mathematics course for elementary teacher candidates.
[claim2]
Findings: Evaluating the claim
Respondents generally agreed that it is important for preparation programs to meet the claim (as articulated in the survey but since slightly revised), "Educator preparation programs, through general education and program-specific requirements, provide elementary teacher candidates with the content and pedagogical knowledge specified in national mathematics education standards that underlie effective instruction." 72% of respondents strongly agreed, and 19% agreed.Support was similarly high from state education agencies (SEAs) (95% agree or strongly agree), compared with teacher preparation programs (TPPs) and institutions of higher education (IHEs) (92% agree or strongly agree). Support was also strong from both those who had taught mathematics to elementary teacher candidates (92%) and those who had not (95%).
The comments were largely positive. A few themes emerged, beyond generally supportive statements.
Several respondents (N=8) wrote comments in support of including both specialized content and mathematical pedagogy in the claim and standard.
Some respondents (N=8) requested that "national math standards" be defined or expanded to include state and local standards.
NCTQ Response
The Math Expert Advisory Panel reviewed this feedback and agreed with the recommendations. NCTQ modified the claim (relevant section underlined) to be:
[content]
Findings: Content of the standard
Respondents agreed that preparation programs should teach aspiring elementary teachers specialized mathematical content knowledge (96% agree or strongly agree) and pedagogical knowledge for teaching mathematics (96% agree or strongly agree).Respondents also generally agreed with the topics underlying the specialized mathematical content knowledge domain (93% of respondents agreed or strongly agreed that the four topics are the "right areas of specialized content knowledge" on which to evaluate elementary programs). There was virtually no difference in the rate of agreement from SEAs versus TPPs and IHEs, or between those who have taught mathematics to elementary candidates and those who have not.
However, some respondents did suggest some revisions to the subtopics within the four main topics.
| Proposed additions to the content of the standard | Example comments | NCTQ response |
| Common content knowledge (N=15) | "A concern I have is that some programs do not require much math content knowledge (i.e. math courses, or math courses for elementary education) for entrance into their programs. Additionally, more and more programs are accepting ANY math course as proof that the student has math content knowledge (i.e. accepting an algebra 2 course from 1982). I think there needs to also be a focus on making sure PSTs have basic math content knowledge." | NCTQ and the Panel agree about the importance of "common content knowledge" (basic math knowledge used by teachers and non-teachers alike). NCTQ addresses this issue primarily in its tracking of state requirements for common content knowledge of prospective teachers, as defined by admissions requirements and general licensure tests. Additionally, NCTQ is analyzing current state math requirements for prospective teachers and will include this analysis in the final report. |
| Fractions, proportions, proportional reasoning (N=6) |
"I agree these are the right areas, but I wonder if specifying the subtopics for N&O would be useful (especially given that one full course is generally devoted to it). For example, is working with fractions and percents with an eye to ratio and proportion included in this topic? Even though these are 6-8 grade topics, I think their connections should be made clear for elementary school teachers, so as not to create unintentional misconceptions."
"I think that fractions should be in a separate domain than Numbers & Operations. There is so much to learn about fractions." |
The topic of fractions is critical. Although "Numbers & Operations – Fractions" is separated from "Numbers & Operations - Base 10" by CCSS-M beginning in Grade 3, we decided to combine. For the utility of the results, NCTQ decided not to divide mathematics content into the 10 CCSS-M topic areas for Grades 1-8 (considering Grades 7-8 as "horizon content knowledge''), but rather on four overarching topics based on NCTM content standards. (NOTE: Based on advice from our Expert Advisory Panel, we combined "Geometry" and "Measurement" into a single topic.) |
| Process standards, problem-solving, and mathematical modeling (N=6) |
"Mathematical modeling is a large component that is left off this list. It is a way of thinking about and utilizing mathematics that could speak to a broader audience. There is a growing body of research about open-ended problem-solving in this context that helps improve mathematical understanding, particularly for those typically underrepresented in mathematics communities."
"These are main topics taught in Mathematics, but I would extend these to the process standards mentioned by NCTM." |
In reviewing the descriptions or syllabi for required mathematics courses, NCTQ analysts do consider references to process standards (problem-solving, reasoning and proof, communication, connections, and representations) in the context of the major topic areas. As defined by NCTM, the process standards are "...ways of acquiring and applying content knowledge" and are not isolated from the content. While "problem-solving" or "reasoning and proof" are not separately coded, they are considered as evidence under the content topic areas.
As NCTQ gathers more evidence from programs regarding the content of the required mathematics courses, we will continue to explore ways to disaggregate information on processes. |
|
A measure of instructor experience & background (N=5)
Several respondents said that instructors' background matters, though differed on what a strong background looks like. |
"Instructors for teacher prep courses should have K-12 teaching experience."
"Mathematics should be taught by professors with mathematics degrees. One must deeply understand the vertical alignment of the concepts." "Invite math education professors to teach math content knowledge rather than asking math professors to teach math content courses for our pre-service elementary math teachers." |
In the development of this standard originally, NCTQ attempted to collect biographical information on faculty to determine their backgrounds and qualifications. It proved impractical for many reasons: the size of some institutions requiring numerous instructors for the same course, turnover among these instructors means that what could be concluded one semester about the instructors was no longer true in the next semester, and most notably we were unable to identify the necessary research needed to defend any recommendation as to the appropriate qualifications of math instructors. While it may make intuitive sense that teachers should have K-12 experience, to the extent possible, all NCTQ standards must rest solidly on consensus research that has been published and peer-reviewed. |
| Equity (N=5) |
"Given the state of the field of elementary mathematics education, any efforts to assess programs that do not consider the preparation of teachers to address issues of equity and inclusion will be extremely limited."
"What is troubling to me is the omission of the word equitable instruction in this standard. It should read "... underlying equitable and effective instruction." or "equity-centered and effective instruction." |
NCTQ agrees with this comment and has modified the claim to reflect this purpose. |
Respondents also identified a few subtopics they believed should be removed from the standard.
| Proposed subtopics to remove from the standard | Example comments | NCTQ response |
| Probability (N=7) |
"In particular probability is not a topic that is taught across most states anymore at K-5 grades and shouldn't be because it relies on an understanding of ratio (not fractions) that is not usually taught till middle school now."
"In the Common Core State Standards for Math, the Probability topic does not occur until 6th grade; therefore our K - 5 teachers are not even teaching it and our 6th-grade teachers continue mostly with data analysis, not true probability itself." |
Two factors explain our position. First, a large number of states consider elementary programs to be K-6. Second, elementary teachers need to have a reasonable understanding of the topics that 'come next'. While it is reasonable to argue that a K-2 teacher needs little exposure to probability, the licenses generally cover teachers through grades 5 and 6. |
| Transformation and symmetry (N=3) |
"I find the bullet under Geometry that focuses on transformations and symmetry surprising since most standards (NCTM and CCSSM) give less attention to these than other geometry content."
|
NCTQ agrees that "transformations" is a mathematical topic typically addressed at the high school level and would not be a common component of a required mathematics course for elementary teachers. However, "symmetry" is a topic that is included later. Programs do not lose points if they do not address transformation (or any other specific subtopic), but time dedicated to transformation is counted under the "Geometry" topic. |
[datasources]
Findings: Data sources and analysis
Respondents had the greatest concerns on the topic of data sources, and specifically the use of course descriptions and syllabi, although the views of most respondents were still favorable to the new standard.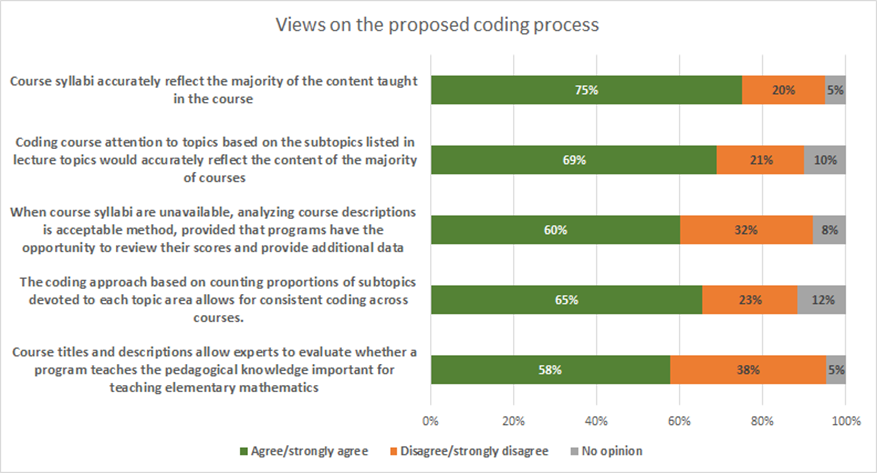
On the question of using course descriptions when syllabi are not available, respondents from higher education institutions were more favorable: 50% of SEAs agreed, compared with 61% of respondents from TPPs and IHEs.
NCTQ Response
NCTQ conducted a number of pilot tests to assess the accuracy of course descriptions before determining its acceptability as a source of evidence. A pilot test evaluated 200 courses where both course descriptions and syllabi were available to arrive at two independent assessments for how much time was spent on each of the five key topics. The two analyses produced similar results on average, within a range of 10 percentage points for each of the five topics. Further, the distribution of program grades under the two approaches was highly correlated, with no notable bias towards either approach. The use of course descriptions in lieu of course syllabi, along with measures of interrater reliability, was reviewed by the Technical Advisory Group (TAG) and elicited no substantial concerns, provided programs have the opportunity to submit additional evidence. More details can be found here and subsequently in the technical manual with the full release of the standard.
[coursetime]
Findings: Course time
Respondents were also asked how much course time should be devoted to each specialized content topic area. The predominant views generally aligned with recommendations from the Expert Advisory Panel.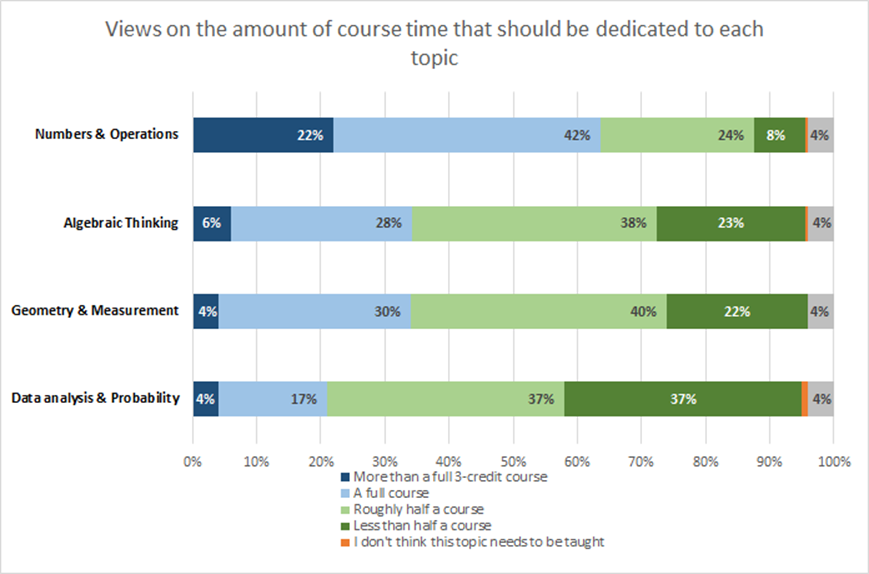
While one might expect an audience of math educators and others highly invested in math education—most of the individuals who replied to the Open Comment invitation—might be tempted to set unrealistically high standards for the number of math courses elementary teachers must take, there is relatively strong alignment with their responses and the final decision by the Expert Advisory Panel.
- 64% of respondents stated that Numbers & Operations merited a full course (45 hours) if not more. The panel set a target of 45 hours, effectively one three-credit course.
- The plurality of respondents (38%) said the amount of course time needed for Algebraic Thinking was half a course, with 34% preferring more and 23% preferring less. The panel set the target at just under half of a 3-credit course, at 20 hours.
- The plurality of respondents (40%) said the amount of course time needed for Geometry & Measurement was half of a course with 34% opting for more time and 22% less. The panel set the target at just over half of a 3-credit course, at 25 hours.
- Respondents were split on the topic of Probability and Statistics; 37% of respondents agreed with the panel that less than half of a course was needed for Probability and Statistics, and 37% recommended roughly half a course. The panel set the target at 15 hours or a third of a 3-credit course.
In general, most respondents agreed that scoring programs based on their course requirements in specialized mathematical content knowledge and pedagogical mathematical content knowledge using course descriptions and syllabi provides a useful picture of whether programs meet the claim (79% agree or strongly agree).
Also, most respondents believed that the Elementary Mathematics standard evaluation process will provide insight into the quality of preparation programs (81% agree or strongly agree). Notably, the agreement was greater among IHEs and TPPS (84%), compared with SEAs (70%). Only three respondents from TPPs or IHEs strongly disagreed with this statement.

[Section3]
Technical Advisory Group Math Convening
In October 2021, NCTQ convened a Technical Advisory Group (TAG) to review key methodological processes related to the revised math standard. The primary issue brought before the TAG was NCTQ's interest in introducing an alternative to looking only at a course syllabus, by considering the more readily available course description. Key topics discussed during the meeting included inter-rater agreement, syllabi, course description comparability, and scoring models. A summary of the TAG's discussion and findings on each of these methodological processes follows.
[interrateragreement]
Interrater Agreement
The TAG examined several calculations of interrater agreement between analysts for 1) course descriptions and 2) course syllabi, as well as the 3) comparability of results from course descriptions and syllabi. The data used for these analyses came from a pilot test of 200 courses. NCTQ partially randomized the assignment of analysts to course descriptions and syllabi to be able to analyze rater agreement. The inter-rater agreement focused on the four content topics and math pedagogy, the five key topics of the standard.At issue was the ability of any of these processes to reach a sufficiently high level of agreement in two main ways. First, did analysts identify whether a course did or did not reference the five key topics; and second, how did the analysts' percentage of instructional time dedicated to a topic as a percentage of the total course correlate?
In order to assess if analysts using course descriptions reached sufficiently strong interrater agreement identifying the five key topics, the TAG looked at the rate of agreement when two analysts were asked to independently render a judgment as to whether any of the five key topics were identifiable in the course description. The rate of agreement in this instance was quite acceptable to the TAG, ranging from 95.0% to 99.5%.
The TAG also reviewed the rate of agreement when two analysts independently coded a course description to determine the amount of instructional time dedicated to a particular topic. On this measure, with the rate of agreement again achieved what the TAG determined was a satisfactory rate of between 0.844 and 0.982.
The TAG then turned its attention to rater agreement among syllabi. They examined the results from two analysts independently determining if any of the five key topics were covered in a course. Agreement between analysts was again satisfactory to the TAG, with agreements ranging from 91.4% to 98.3%.
Finally, the TAG reviewed the results of having two analysts independently determine the percentage of instructional time dedicated to a topic, using a syllabus. The rate of interrater agreement was again satisfactory to the TAG, ranging between 0.931 and 0.985.
Table 1. Interrater Agreement
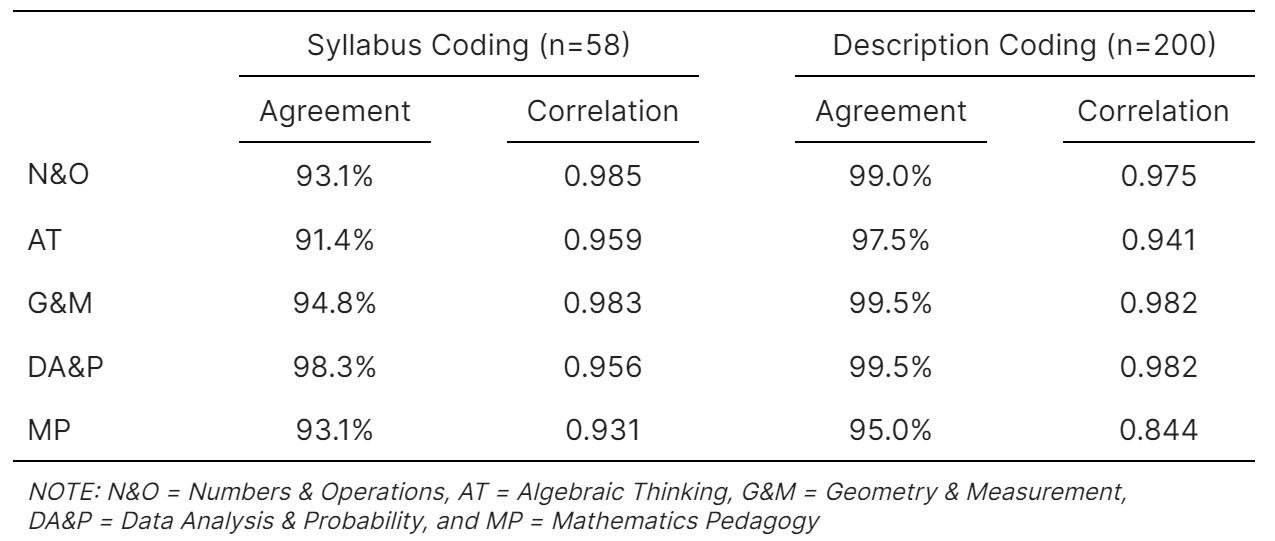
Based on these results, TAG members unanimously agreed that the interrater agreement among analysts using either syllabi or course descriptions was sufficient. Still, given the concerns over the brevity of course descriptions and that this will be the first time course descriptions will be used, the TAG affirmed NCTQ's plan to have all course descriptions independently analyzed by two analysts with a third analyst adjudicating any significant disagreements.
[syllabi]
Syllabi and course description comparability
The TAG then examined the consistency between ratings when both course descriptions and syllabi were being used, to ensure that the results were comparable. Syllabi, by design, includes more detailed information regarding both the topics that are covered and the amount of instructional time dedicated to each of those topics. Course descriptions are high-level summaries of the topics covered by a course.For this analysis of comparability, the panel examined the coding results from 185 math courses which NCTQ had both the course description and the syllabus.
The coding results were compared from having two analysts independently code whether a key topic area was referenced in the course description (averaging the results of two analysts) with the result of an analyst coding the course using a syllabus.
The agreement rate between the two was sufficient with the exception of one topic, Algebraic Thinking.
- Geometry & Measurement: 89%
- Numbers & Operations: 83%
- Data Analysis & Probability: 82%
- Algebraic Thinking: 67%
Even given the lower agreement rate for Algebraic Thinking, the TAG concluded that the reliability of the coding was adequate for the level of this analysis and that the problem of lack of agreement between description and syllabus coding was most likely a feature of a topic getting scant treatment in a course.
The TAG considered the rate of agreement to be generally sufficient to allow the use of a course description when a syllabus was not available, especially in that programs would be given the opportunity to review their score and make a decision to provide a syllabus. The TAG agreed with the Expert Advisory Panel that NCTQ should make every effort to obtain syllabi from teacher preparation programs and supported efforts to reach back out to programs with a second opportunity to provide materials.
[scoring]
Scoring models
For the four content topic areas and mathematics pedagogy, the TAG supported a grading structure in which the instructional hours for each topic are counted within each course and summed for the program. Under this scoring approach, programs receive credit for the number of instructional hours they require up to the target. The sum of the five topic values then being used to determine the overall coverage.TAG members considered an alternative approach to the mathematics pedagogy calculation, in which points would be awarded on an all-or-nothing basis should the instructional hour target have been met. The more granular approach was ultimately accepted to align mathematics pedagogy with the other four topics by providing programs with the same level of feedback. Consideration was also given to a scoring structure under which the same number of points would be awarded under each of the topic areas. This idea was rejected due to its effect of increasing the relative value of an instructional hour in one topic area compared to another.
Elementary Mathematics Technical Advisory Group
Dr. Ed Crowe
Chief Executive Officer, TPI-US
Dr. Kristen Huff
Vice President, Assessment and Research at Curriculum Associates
Dr. Cory Koedel
Professor of Economics and Public Policy, University of Missouri
Dr. William Schmidt
University Distinguished Professor and Founder and Director of the Center for the Study of Curriculum Policy, Michigan State University
Dr. Amber Willis
Formerly TeachingWorks, currently Program Director, Deans for Impact

[Section4]
Math Expert Advisory Panel
The Math Expert Advisory Panel (EAP) met twice, once in May 2021 and again in November 2021.
The purpose of the May meeting was to review and provide feedback on the math topics and data sources for the standard.
In November, the EAP met to review pilot data, feedback from the Open Comment period, and recommendations from the Technical Advisory Group (TAG). Prior to the meeting, the Panel provided recommendations for the sub-topics under each of the four content areas that it had confirmed in its May 2021 meeting (Numbers & Operations, Algebraic Thinking, Geometry & Measurement, and Probability and Statistics). The purpose of identifying the subtopics under each of the topics was to provide NCTQ math analysts specific guidance for determining how to appropriately code syllabi and course descriptions.
During the November meeting, the Panel provided input on four key issues to finalize the standard: 1) determining how math pedagogy would factor into a program's grade; 2)setting the target instructional hours for each major topic area; 3) defining an "A" program; and, 4) creating a scoring model that accommodated the overlap in topics between Numbers & Operations and Algebraic Thinking. Each of the recommended solutions is explained here.
[pedagogy]
Math pedagogy
Based on the recommendations of the Expert Advisory Panel and the Technical Advisory Group (TAG), mathematics pedagogy will be evaluated by estimating the instructional hours a program's coursework dedicates to this topic, similar to the four content areas. For all five topics, programs earn points based on the number of instructional hours allocated to the topic (up to but not exceeding the target threshold), as a share of the total instructional hours available.[hours]
Target instructional hours
In order to assess all types of programs, NCTQ needed to establish a constant unit of measurement, "instructional hours," as opposed to "half of a course" since courses consist of different numbers of credit hours. Nevertheless, as most institutions use a 3-credit format for their courses with each credit representing 15 instructional hours, the following conversion on the chart below may be useful.After considering prior work343 and all of the feedback, including open comment responses and the Panel recommendations, NCTQ settled on the following number of minimal instructional hours as the target programs ought to achieve over a combination of coursework:
| Numbers & Operations | Algebraic Thinking | Geometry & Measurement | Data Analysis & Probability | Math Pedagogy | Total |
| 45 hours | 20 hours | 25 hours | 15 hours | 45 hours | 150 hours |
| One 3-credit course | Just under half of a 3-credit course | Just over half of a 3-credit course | One third of a 3- credit course | One full 3-credit course | 10 credits |
The process of setting the appropriate number of instructional hours was originally conducted in 2008 when NCTQ first devised this standard (see No Common Denominator, pg. 24) for a full description of this process). These allocations were again reviewed for this revision, with only modest modifications made to those original targets and still concluding with a recommendation of roughly four 3-credit courses to cover both the content and the pedagogical knowledge deemed necessary.
[Aprogram]
Definition of an "A" program
The Panel recommended programs should reach at least 90% of the target instructional hours under each topic in order to qualify for a grade of A. Given that these are intended as minimal thresholds, the rule is relatively immutable, meaning that even programs that address 90% or more of the cumulative instructional hours in all but one area still would not qualify for an A.[overlap]
Resolving overlap between Numbers & Operations and Algebraic Thinking
The Panel wrestled with some of the challenges discerning the instructional hours dedicated to Algebraic Thinking, even considering at one point combining Numbers & Operations and Algebraic Thinking into one topic. Coursework descriptions often combine Numbers & Operations and Algebraic Thinking concepts making it difficult to separate when determining overall grades for teacher preparation programs. This may occur because student standards (such as the Common Core State Mathematics Standards (CCSS-M)) combine Operations and Algebraic Thinking through the mid-elementary grades, with Algebra becoming more of a separate topic in later grades.The Panel ultimately agreed that it was important for programs to be provided feedback specifically on Algebraic Thinking, but did not want programs to be unfairly graded given this challenge.
The Panel recommended combining Numbers and Operations and Algebraic Thinking for grading purposes, and NCTQ affirmed this approach as the preferred solution, as it is most likely to avoid penalizing programs for any ambiguity that exists due to overlapping topics between Numbers & Operations and Algebraic Thinking.
We will continue to monitor and evaluate the approaches TPPs are taking to address Algebraic Thinking and consider revisions to the standard to better provide programs with feedback to strengthen coverage of critical mathematics topics.
Math Expert Advisory Panel Members
Dr. Jennifer Bay-Williams
Professor of Mathematics Education, University of Louisville
Ms. Alicia Brown
Senior Director, K-8 Mathematics, Detroit Public Schools Community District
Mr. Steven Leinwand
Principal Research Analyst, American Institutes for Research
Dr. Denise Padilla
Elementary Education Professor and Department Chair, Great Basin College
Dr. Michael Savoy
Vice President of Programs, TeachPlus
Dr. Amber Willis
Formerly TeachingWorks, currently Program Director, Deans for Impact
Anonymous Members
Mathematician and contributor to the MET Study representative
North Carolina Agricultural & Technical State University representative
Teacher of the Year representative, math specialist
University representative, Mid-Atlantic region
University representative, Southern-U.S. region
[endnotes]
Endnotes



